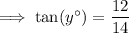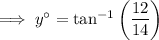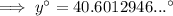Question

3.) x =
X
21
_y=_
43°
121
14
4.)

Answer 1

If the triangles are similar:

• x = 18
• y = 43

If the triangles are right triangles:

• x = 19.6
• y = 40.6

Explanation:

Note: As the question does not state if the triangles are similar triangles or right triangles, I have provided the answer for both options.

--------------------------------------------------------------------------------

If the triangles are similar

In similar triangles, corresponding interior angles are congruent.

Therefore, y = 43.

In similar triangles, corresponding sides are always in the same ratio.

`\implies \sf 21:14=x:12`

`\implies \sf (21)/(14)=(x)/(12)`

`\implies \sf x=(21 \cdot 12)/(14)`

`\implies \sf x=18`

--------------------------------------------------------------------------------

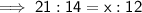
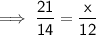
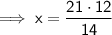
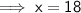
If the triangles are right triangles

Trigonometric ratios

`\sf \sin(\theta)=(O)/(H)\quad\cos(\theta)=(A)/(H)\quad\tan(\theta)=(O)/(A)`

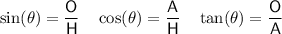
where:

• θ is the angle.
• O is the side opposite the angle.
• A is the side adjacent the angle.
• H is the hypotenuse (the side opposite the right angle).

Note: Assuming the triangles are right triangles.

Triangle x

Given:

• θ = 43°
• O = x
• A = 21

Substitute the given values into the tan trigonometric ratio and solve for x:

`\implies \tan(43^(\circ))=(x)/(21)`

`\implies x=21\tan(43^(\circ))`

`\implies x=19.5828168...`

`\implies x=19.6 \sf \; \;(nearest\;tenth)`

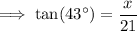
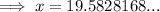
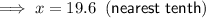
Triangle y

Given:

• θ = y°
• O = 12
• A = 14

Substitute the given values into the tan trigonometric ratio and solve for y:

`\implies \tan(y^(\circ))=(12)/(14)`

`\implies y^(\circ)=\tan^(-1)\left((12)/(14)\right)`

`\implies y^(\circ)=40.6012946...^(\circ)`

`\implies y=40.6\;\; \sf (nearest\;tenth)`

Answer 2

• x = 18, y = 43°

----------------------------------

Given

• Similar triangles with missing dimensions

Find x using equal ratios of corresponding sides

• x/12 = 21/14
• x /12 = 3/2
• x = 12*3/2
• x = 18

Corresponding angles are congruent:

• y = 43°