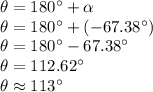Answer:
C) 113°
Explanation:
The direction angle for a position vector
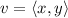 is
is
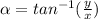 plus a correction based on the quadrant (more on that later).
plus a correction based on the quadrant (more on that later).
Hence:
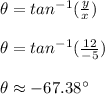
We are not done here, however, as we need to account for which quadrant the vector is located in. Since v=⟨-5, 12⟩ is located in Quadrant II, then the direction angle must also be in Quadrant II.
Therefore, we use the formula
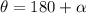 to account for this:
to account for this: