Question

A 6.0-kg block initially at rest is pulled to the right along a frictionless, horizontal

surface by a constant horizontal force of magnitude 12 N. Find the block’s speed after
it has moved through a horizontal distance of 3.0 m.

Answer 1

• 4 m/s

Step-by-step explanation:

Force, mass and acceleration are related to each other as ,

`\implies \boxed{\rm Force = mass * acceleration} \\`

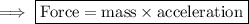
Here force is 12N and mass is 6kg. Hence the acceleration of the block will be;

`\implies a = (F)/(m) \\`

`\implies a = (12N)/(6kg) \\\\`

`\implies a = 2\ m/s^2 \\\\`

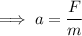
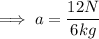
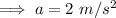
Now the block was initially at rest so its initial velocity would be 0m/s . Now after it is displaced 3m we need to find the speed of the block.

We can use Third equation of motion as ;

`\implies \boxed{ 2as = v^2 - u^2}\\`

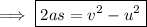
where the symbols have their usual meaning.

On substituting the respective values, we have;

`\implies 2* 2\ m/s^2 * 3\ m = v^2-(0\ m/s)^2 \\\\`

`\implies 12\ m^2/s^2 = 3v^2 \\\\`

`\implies v= \sqrt{ (12)/(3)} m/s\\\\`

`\implies \boxed{ v = 4\ m/s} \\`

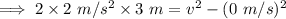
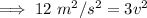
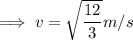
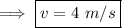
Henceforth the final speed is 4m/s .