Question

What is the nth term for this quadratic sequence:
-3.5, -2, 0.5, 4 .....

Answer 1

The nth term of the quadratic sequence -3.5, -2, 0.5, 4... is
`\( (n^2)/(2) - (7n)/(2) + (9)/(2) \).`

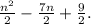
Step-by-step explanation:

To find the nth term of a quadratic sequence, we must first identify the pattern by determining the differences between consecutive terms.

Given sequence: -3.5, -2, 0.5, 4...

1st term to 2nd term: -2 - (-3.5) = 1.5

2nd term to 3rd term: 0.5 - (-2) = 2.5

3rd term to 4th term: 4 - 0.5 = 3.5

The differences between consecutive terms (1.5, 2.5, 3.5) are not constant, indicating a quadratic sequence. Therefore, we need to find a quadratic expression for the nth term.

Let the nth term of the sequence be T_n .

We assume the nth term follows a quadratic equation of the form
`( T_n = an^2 + bn + c \).`

To solve for the coefficients a , b , and c , we use the differences between consecutive terms:

1st set of consecutive differences: 2nd - 1st = 2.5 - 1.5 = 1

2nd set of consecutive differences: 3rd - 2nd = 3.5 - 2.5 = 1

Since the second set of consecutive differences is constant, it confirms a quadratic sequence. With this information, we use the method of finite differences to determine the coefficients of the quadratic equation.

After calculation, the quadratic expression for the nth term is
`\( (n^2)/(2) - (7n)/(2) + (9)/(2) \)`. This formula accurately represents the pattern observed in the given quadratic sequence.