Question

3. A solid metal right circular cylinder of radius r cm and height h cm. The total

surface area of the cylinder is 600 cm2

. The volume of the cylinder is V cm3

(a) Show that V = 300r − πr^3


Given that r can vary,
(b) (i) use calculus to show that the exact value of r for which V is a
maximum is r = root 100 by π

(ii) justify that this value of r gives a maximum value of V
The cylinder is melted down and reformed into a sphere of radius p cm.
(c) Find, to one decimal place, the greatest possible value of p.

Answer 1

(a) V = 300r -πr³ cm³

(b) r = √(100/π) cm

(c) p ≈ 6.5 cm

Explanation:

Given a cylinder with a surface area of 600 cm², you want to show (a) that its volume is V=300r -πr³, and (b) that the radius for maximum volume is r=√(100/π). You also want to find the radius of a sphere with that same maximum volume.

Formulas

The formulas for the area and volume of a cylinder and the radius of a sphere are ...

A = 2πr(r +h) . . . . . . surface area of a cylinder of radius r, height h

V = πr²h . . . . . . . . . volume of a cylinder of radius r, height h

r = ∛(3V/(4π)) . . . . radius of a sphere with volume V

(a) cylinder volume

Solving the cylinder surface area formula for height, we get ...

`A=2\pi r(r+h)\\\\(A)/(2\pi r)=r+h\\\\h=(A)/(2\pi r)-r=(600)/(2\pi r)-r=(300)/(\pi r)-r`

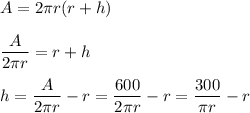
Using this value in the volume formula, we find the cylinder volume to be ...

`V=\pi r^2h\\\\V=\pi r^2\left((300)/(\pi r)-r\right)\\\\\boxed{V=300r-\pi r^3}`

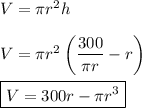
(b) cylinder radius

The volume of the cylinder is maximized when its derivative with respect to radius is zero:

V' = 300 -3πr² = 0

100 = πr² . . . . . . . . . . divide by 3, add πr²

r = √(100/π) . . . . . . . divide by π, take the square root

The radius of the cylinder with surface area 600 cm² and maximum volume is r = √(100/π).

(c) sphere radius

The volume of the cylinder with maximum volume is ...

V = r(300 -πr²) = r(300 -100) = 200r = 200√(100/π)

V = 2000/√π

The radius of the sphere with the same volume is ...

`p=\sqrt[3]{(3V)/(4\pi)}=\sqrt[3]{(3(2000)/(√(\pi)))/(4\pi)}=\frac{\sqrt[3]{1500}}{√(\pi)}\approx6.45836\\\\\boxed{p\approx6.5\text{ cm}}`