Question

Use Pythagoras' theorem to calculate the length of BF in the right- angled triangular prism below. Give your answer in centimetres (cm) to 1 d.p. 14 cm D E 19 cm C 9 cm B F Not drawn accurately​

Answer 1

Applying Pythagoras' theorem to the right-angled triangular prism, BF =
`√(( BC^2 + CD^2) )= \sqrt{(14^2 + 9^2)` = 17.16 cm.

To calculate the length of BF in the right-angled triangular prism below using Pythagoras' theorem, we need to identify the two sides that are perpendicular to BF. These are sides BC and CD.To calculate this, we use Pythagoras' theorem, which states that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

In this case, the hypotenuse is BF and the other two sides are BC and CD. We are given that BC = 14 cm and CD = 9 cm, so we can substitute these values into Pythagoras' theorem. Therefore, we can use the following equation:

`BF^2 = BC^2 + CD^2`

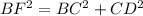
We are given that BC = 14 cm and CD = 9 cm, so we can substitute these values into the equation:

`BF^2 = 14^2 + 9^2\\BF^2 = 294`

`BF = \sqrt{(294)`

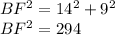
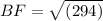
BF = 17.16 cm (to 1 d.p.)

Therefore, the length of BF is 17.16 cm.