Question

Match the variables and constants from the modified form of Kepler's third law to their correct units.

Answer 1

Kepler's third law relates the orbital period T of a celestial body to the semi-major axis a of its orbit. The modified form of Kepler's third law can be expressed as
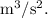`\(\text{m}^3/\text{s}^2\).`, where k is a constant.

To match the variables and constants with their units:

1. T: Orbital period, measured in seconds (s).

2. a: Semi-major axis, measured in meters (m).

3. k: Constant, unit depends on the units chosen for T and a. If T is in seconds and a is in meters, k will have units of
`\(\text{m}^3/\text{s}^2\).`

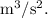
Therefore:

- \(T\) is in seconds (s),

- \(a\) is in meters (m),

- k is in
`\(\text{m}^3/\text{s}^2\)` (or adjusted based on the chosen units for T and a.