Answer: The probability that the no. is divisible by 4 is 0.225 .
Explanation:
First three-digit number: a = 100
Last digit number: l = 996
Common difference: d = 4
Formula: l=a+(n-1)d
Substitute all values, we get
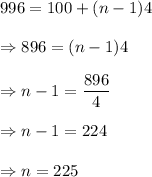
i.e. there are 225 three digit numbers divisible by 4.
Total 3-digit numbers = 1000
The probability that the no. is divisible by 4 =
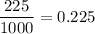
Hence, the probability that the no. is divisible by 4 is 0.225 .