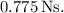The magnitude of the impulse acting on the ball during the hit is approximately
To find the magnitude of the impulse acting on the ball, you can use the impulse-momentum theorem, which states:
![\[ \text{Impulse} = \Delta p \]](https://img.qammunity.org/2024/formulas/physics/college/gkufblqfwbr2xd0wk4m783fvx5i9uli3tc.png)
where
 is the change in momentum.
is the change in momentum.
The momentum (p) is given by the product of mass (m) and velocity (v):
![\[ p = m \cdot v \]](https://img.qammunity.org/2024/formulas/physics/high-school/3xeirbdaw9936zab35zjthgge9hstj451r.png)
The change in momentum is then:
![\[ \Delta p = p_{\text{final}} - p_{\text{initial}} \]](https://img.qammunity.org/2024/formulas/physics/college/l4x8dhmz92myctlcku8v3wgiopyowfp8wt.png)
For the incoming baseball:
![\[ p_{\text{initial}} = m_{\text{incoming}} \cdot v_{\text{incoming}} \]](https://img.qammunity.org/2024/formulas/physics/college/8wqecy1be20kj65dnrvda8zyyrx446wf3o.png)
For the outgoing baseball:
![\[ p_{\text{final}} = m_{\text{outgoing}} \cdot v_{\text{outgoing}} \]](https://img.qammunity.org/2024/formulas/physics/college/tfro0xkaf874hnzb9mc3qu10wm0d2ppkho.png)
The magnitude of the impulse is the absolute value of the change in momentum:
![\[ \text{Impulse} = |\Delta p| \]](https://img.qammunity.org/2024/formulas/physics/college/w22yvcbths9ec355dvx7hw48l2kvn29ht5.png)
Given:
-
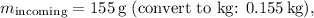
-
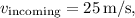
-
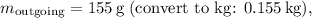
-
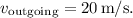
Calculate
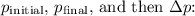
![\[ p_{\text{initial}} = 0.155 \, \text{kg} \cdot 25 \, \text{m/s} \]](https://img.qammunity.org/2024/formulas/physics/college/cf2hg7qdt7ism49mpsf3lbjc0kvb8pu0ob.png)
![\[ p_{\text{initial}} = 3.875 \, \text{Ns} \]](https://img.qammunity.org/2024/formulas/physics/college/y5a7ea7ckylfuicn93v2tteh0ex3a8lau6.png)
![\[ p_{\text{final}} = 0.155 \, \text{kg} \cdot 20 \, \text{m/s} \]](https://img.qammunity.org/2024/formulas/physics/college/spgckp19ze4fy04lock9v1p74yetmsbuy5.png)
![\[ p_{\text{final}} = 3.1 \, \text{Ns} \]](https://img.qammunity.org/2024/formulas/physics/college/ey9if7yh8od1as7yp0313qstnbjmqrn15g.png)
![\[ \Delta p = |3.1 \, \text{Ns} - 3.875 \, \text{Ns}| \]](https://img.qammunity.org/2024/formulas/physics/college/9ti14kf1tlpzknlg59bznodfew2ltww4ei.png)
![\[ \Delta p \approx 0.775 \, \text{Ns} \]](https://img.qammunity.org/2024/formulas/physics/college/zqi8snp3vs2ay029lgt3vei3v9gge50axx.png)
Therefore, the magnitude of the impulse acting on the ball during the hit is approximately