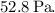The pressure difference (
 ) in the enlarged region of the aorta exceeds the pressure in the normal region by approximately
) in the enlarged region of the aorta exceeds the pressure in the normal region by approximately
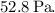
The relationship between pressure, velocity, and cross-sectional area in fluid flow is described by Bernoulli's equation:
![\[ P + (1)/(2)\rho v^2 + \rho gh = \text{constant} \]](https://img.qammunity.org/2024/formulas/physics/college/zwidafwfdscg7b0jd5g86045jjwp2fs9ti.png)
where:
- P is pressure,
-
 is the fluid density,
is the fluid density,
- v is the fluid velocity,
- g is the acceleration due to gravity,
- h is the height above some reference point.
Since the aorta is horizontal, we can ignore the gravitational term (
 ).
).
For a normal portion of the aorta (subscript 1), and an enlarged portion (subscript 2), Bernoulli's equation becomes:
![\[ P_1 + (1)/(2)\rho v_1^2 = P_2 + (1)/(2)\rho v_2^2 \]](https://img.qammunity.org/2024/formulas/physics/college/1f8vwu7xyip9q5i10oyi0fjzk48yneal8l.png)
Given that
 , the relationship between velocities is
, the relationship between velocities is
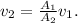
Substitute this relationship into Bernoulli's equation:
![\[ P_1 + (1)/(2)\rho v_1^2 = P_2 + (1)/(2)\rho\left((A_1)/(A_2)v_1\right)^2 \]](https://img.qammunity.org/2024/formulas/physics/college/g0szjox81n5f15rbx204j0nndlfiqjwwrp.png)
Now, we are interested in the difference in pressure (
 ):
):
![\[ P_2 - P_1 = (1)/(2)\rho v_1^2 - (1)/(2)\rho\left((A_1)/(A_2)v_1\right)^2 \]](https://img.qammunity.org/2024/formulas/physics/college/963xhymervhao23pl79vmr2jffbem89bnj.png)
![\[ P_2 - P_1 = (1)/(2)\rho v_1^2\left(1 - \left((A_1)/(A_2)\right)^2\right) \]](https://img.qammunity.org/2024/formulas/physics/college/7u6qn4swdt9ghlo5i6wxv5dwsh5qdsywlq.png)
![\[ P_2 - P_1 = (1)/(2)\rho v_1^2\left(1 - \left((A_1)/(1.7A_1)\right)^2\right) \]](https://img.qammunity.org/2024/formulas/physics/college/wacn9xi53g2yyrjlljmd0fwwb5ufiep0v4.png)
![\[ P_2 - P_1 = (1)/(2)\rho v_1^2\left(1 - \left((1)/(1.7)\right)^2\right) \]](https://img.qammunity.org/2024/formulas/physics/college/twbohksj6b1cg6c2ecdpn47mwrmvu6o4rn.png)
![\[ P_2 - P_1 = (1)/(2)\rho v_1^2\left(1 - (1)/(2.89)\right) \]](https://img.qammunity.org/2024/formulas/physics/college/r8949adkev8vgfy2ejd6witljy3brrfjtq.png)
![\[ P_2 - P_1 = (1)/(2)\rho v_1^2 * (1.89)/(2.89) \]](https://img.qammunity.org/2024/formulas/physics/college/1cg894k7j2y7kai7rqu5y0h4bt95m53tem.png)
Given that
 , substitute these values:
, substitute these values:
![\[ P_2 - P_1 = (1)/(2) * 1060 * (0.40)^2 * (1.89)/(2.89) \]](https://img.qammunity.org/2024/formulas/physics/college/p5zw89pa3cvmrkzqwzzytqgew2x6yi3ow8.png)
![\[ P_2 - P_1 \approx 52.8 \, \text{Pa} \]](https://img.qammunity.org/2024/formulas/physics/college/xq9fi8fco5deyetjrd4yxwkx5uwvr2wq63.png)
Therefore, the pressure difference (
 ) in the enlarged region of the aorta exceeds the pressure in the normal region by approximately
) in the enlarged region of the aorta exceeds the pressure in the normal region by approximately