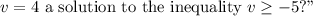Question

1. v≥-5;4
is each number following the inequality a solution of the given inequality?

Answer 1

Yes,
`\(v = 4\)` is a solution to
`\(v \geq -5\).` Substituting
`\(v = 4\)` into the inequality yields a true statement, confirming its validity within the solution set.

The inequality
`\(v \geq -5\)` asserts that the variable
`\(v\)` must be greater than or equal to -5. To address the question of whether
`\(v = 4\)` is a solution, we substitute
`\(v = 4\)` into the inequality:
`\(4 \geq -5\)`. This statement is indeed true, as 4 is greater than -5. Therefore,
`\(v = 4\)`is a valid solution to the inequality.

This outcome aligns with the general understanding of inequalities, where any value greater than or equal to the specified bound satisfies the inequality. In this context, the solution set includes all real numbers greater than or equal to -5.

The broader significance of this process lies in understanding and verifying solutions to inequalities. It provides a method for determining whether a particular value for the variable meets the specified conditions. Such inquiries are fundamental in mathematical modeling, decision-making processes, and various real-world applications where conditions must be met for a statement or system to be valid.

The probable question maybe:

"Is
`\( v = 4 \) a solution to the inequality \( v \geq -5 \)?`