Question

What is the y-coordinate of the point that divides the directed line segment from J to K into a ratio of 2:3? –6 –5 5 7tion m over m n endfraction) (x 2 minus x 1) x 1 y = (startfraction m over m n endfraction) (y 2 minus y 1) y 1 where is the gym? 9th street and 10th avenue 12th street and 12th avenue 14th street and 12th avenue 15th street and 14th avenue

Answer 1

The y-coordinate of the point dividing the line segment from J to K in a 2:3 ratio is
`\(-(4)/(5)\)`. The formula used considers the ratio and y-coordinates of J and K.

The formula for finding the y-coordinate
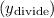`(\(y_{\text{divide}}\))` that divides the directed line segment from point J to K into a ratio of m:n is given by:

`\[ y_{\text{divide}} = (m \cdot y_2 + n \cdot y_1)/(m + n) \]`

where:

- m and n are the parts into which the line segment is divided,

- y_1 and y_2 are the y-coordinates of points J and K, respectively.

In this case, the ratio is 2:3, so m = 2 and n = 3. The coordinates of points J and K are not provided, so let's assume they are
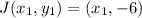`\(J(x_1, y_1) = (x_1, -6)\)` and
`\(K(x_2, y_2) = (x_2, 7)\)`.

Now, substitute the values into the formula:

`\[ y_{\text{divide}} = (2 \cdot 7 + 3 \cdot (-6))/(2 + 3) \]\[ y_{\text{divide}} = (14 - 18)/(5) \]\[ y_{\text{divide}} = (-4)/(5) \]`

So, the y-coordinate of the point that divides the directed line segment from J to K into a ratio of 2:3 is
`\(-(4)/(5)\)`.

Question:

What is the y-coordinate of the point that divides the directed line segment from J to K into a ratio of 2:3? y = (StartFraction m Over m + n EndFraction) (y 2 minus y 1) + y 1 –6 –5 5 7