The simplified expression is
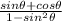 .
.
To simplify the expression
 , let's follow a similar approach as before:
, let's follow a similar approach as before:
Combine the fractions in the numerator:
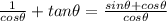
Invert and multiply by the reciprocal of the denominator:

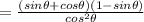
Expand the numerator:
=
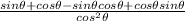
Combine like terms:
=
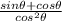
Now, if you want to express this in terms of trigonometric identities, you can use the Pythagorean identity
 to replace
to replace
 in the denominator:
in the denominator:
=
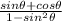
Therefore, the simplified expression is
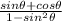 .
.