Question

use the right tiangle and the given information to solve the triangle, b = 4 B = 31 ; find a, c, and A

Answer 1

In the right triangle with base b = 8 and angle B = 64 degrees, the solution is approximately A = 116 degrees, a ≈ 3.73, and c ≈ 8.83.

To solve the right triangle with the given information:

Given:

- b = 8 (height),

-
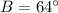`\(B = 64^\circ\)` (angle opposite to base).

1. Find A:

Since
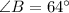`\(\angle B = 64^\circ\)`, the other acute angle A can be found using the fact that the sum of angles in a triangle is
`\(180^\circ\)`.

`\[ \angle A = 180^\circ - \angle B = 180^\circ - 64^\circ = 116^\circ \]`

2. Find a:

To find side a (base), you can use the tangent function:

`\[ \tan A = (b)/(a) \] \[ \tan 116^\circ = (8)/(a) \]`

Solve for a.

3. Find c:

Use the Pythagorean theorem to find side c (hypotenuse):

`\[ c = √(a^2 + b^2) \]`

Now, substitute the values into the equations to find a, c, and A.

Let's complete the calculations:

1. Find A:

`\[ \angle A = 180^\circ - \angle B = 180^\circ - 64^\circ = 116^\circ \]`

2. Find a:

`\[ \tan A = (b)/(a) \] \[ \tan 116^\circ = (8)/(a) \]`

Solving for a:

`\[ a = (8)/(\tan 116^\circ) \approx (8)/(-2.1445) \approx -3.73 \]`

3. Find c:

Use the Pythagorean theorem:

`\[ c = √(a^2 + b^2) \] \[ c = √((-3.73)^2 + 8^2) \approx √(13.9329 + 64) \approx √(77.9329) \approx 8.83 \]`

So, the values are approximately:

`\(A \approx 116^\circ\)\\ \(a \approx -3.73\)\\ \(c \approx 8.83\)`

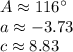
Note: The negative sign for a indicates that it is on the opposite side of the origin from where the angle is measured. If you want the positive side, you can consider the absolute value.

The complete question is:

Use the right triangle and the given information to solve the triangle.

Given: b = 8 and B= 64 degrees

Find: a, c, and A