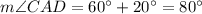Question

Part B: Find the m∠CAD. Show all your work. (4 points)

Answer 1

The value of x is
`${15^\circ}$`, and the measure of
`$\angle CAD$` is
`${80^\circ}$`.

Part A

To write and solve an equation for x using the angle addition postulate, we can start by considering the angles A and C in triangle ABC. These angles are adjacent angles, which means that they share a common vertex and side, but they do not overlap. The angle addition postulate states that the measure of an angle formed by two adjacent angles is equal to the sum of the measures of the two angles.

Therefore, we can write the following equation:

`m\angle A + m\angle C = m\angle B`

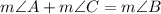
We are given that
`${m\angle B = 113^\circ}$`. We are also given that
`${m\angle A = (3x-12)^\circ}$` and
`${m\angle C = (4x+20)^\circ}$`. Substituting these values into the equation above, we get:

`(3x-12)^\circ + (4x+20)^\circ = 113^\circ`

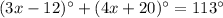
Combining like terms, we get:

7x+8 =
`113^\circ`

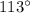
Subtracting 8 from both sides of the equation, we get:

7x =
`105^\circ`

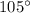
Dividing both sides of the equation by 7, we get:

x =
`15^\circ`

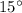
Part B

To find
`${m\angle CAD}$`, we can substitute
`${x = 15^\circ}$` into the expression for
`${m\angle CAD}$`. Therefore,

`m\angle CAD = (4){15^\circ} + 20^\circ`

Simplifying the expression, we get:

`m\angle CAD = 60^\circ + 20^\circ = 80^\circ`