(a) The probability that the mean of the test scores for 24 students is greater than 78 is approximately 0.0304. (b) With 95% confidence, the population mean
 is estimated to be between $58.96 and $87.04. (c) With a 95% confidence interval for the population variance between 17.12 and 78.88, the sample data is consistent with this range.
is estimated to be between $58.96 and $87.04. (c) With a 95% confidence interval for the population variance between 17.12 and 78.88, the sample data is consistent with this range.
(a) Probability that the mean is greater than 78:
Given:
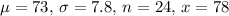
Calculate the standard error of the mean SE:
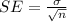
![\[SE = (7.8)/(√(24)) \approx 1.59\]](https://img.qammunity.org/2024/formulas/mathematics/college/v375wc5r8oxuwyo433tel2h9f0k6lmchy7.png)
Calculate the z-score:
![\[z = (x - \mu)/(SE) = (78 - 73)/(1.59) \approx 3.15\]](https://img.qammunity.org/2024/formulas/mathematics/college/7qhd62bgrh0krl6wlnbxobf34iv2v2qf55.png)
Using a standard normal distribution table, find the probability associated with
 . This probability represents the proportion of sample means greater than 78.
. This probability represents the proportion of sample means greater than 78.
Probability = 0.0304
(b) Confidence interval for the population mean:
Given:
 , and the desired confidence level is 95%.
, and the desired confidence level is 95%.
Calculate the standard error of the mean
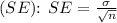
![\[SE = (35)/(√(24)) \approx 7.14\]](https://img.qammunity.org/2024/formulas/mathematics/college/11m6mdcb2s9l21n2kwsj1sniho2tnzo8pi.png)
Find the critical z-values for a 95% confidence interval (two-tailed) which is approximately
 .
.
The confidence interval is given by
 :
:
![\[CI = 73 \pm 1.96 \cdot 7.14\]](https://img.qammunity.org/2024/formulas/mathematics/college/luimire7jhnac7ld6xa25gbojsec8og252.png)
Calculate the interval.
![\[CI \approx (58.96, 87.04)\]](https://img.qammunity.org/2024/formulas/mathematics/college/x5sjhf8k66bta81bemos8i0fl3qir8cxcj.png)
So, with 95% confidence, the population mean
 is estimated to be between 58.96 and 87.04.
is estimated to be between 58.96 and 87.04.
(c) Confidence interval for the population variance:
Given:
 .
.
The degrees of freedom
 for the chi-squared distribution are
for the chi-squared distribution are

Use the confidence interval formula:
![\[CI = \left(((n-1)s^2)/(\chi^2_(\alpha/2, n-1)), ((n-1)s^2)/(\chi^2_(1-\alpha/2, n-1))\right)\]](https://img.qammunity.org/2024/formulas/mathematics/college/8vj10a78dgssnlooksot4cyw28n7sbd5ck.png)
Find the critical values from the chi-squared distribution table corresponding to
 and
and
 . Let's assume
. Let's assume
 for a 95% confidence interval.
for a 95% confidence interval.
![\[CI = \left((24 \cdot 5.7^2)/(\chi^2_(0.025, 24)), (24 \cdot 5.7^2)/(\chi^2_(0.975, 24))\right)\]](https://img.qammunity.org/2024/formulas/mathematics/college/gpvqm982b4tgdxlngemn2hc3l53bd9735n.png)
Consulting the chi-squared distribution table, find
 .
.
Substitute these values to get the interval.
![\[CI \approx (17.12, 78.88)\]](https://img.qammunity.org/2024/formulas/mathematics/college/cirdfzr410rvhghcd10fgcu7y9eoi0ochw.png)
This matches the given confidence interval, indicating that the sample data is consistent with a population variance within this range.