Question

What is the value of r?

Answer 1

Since the image shows the following:
`1fr > 0and\[\sqrt[3]{(9r)/(2)}=(1)/(2)r\]`and the question asks for the value of r, then the answer is r = 1.

The value of r in the image is **1**.

To solve for r, we can start by cubing both sides of the equation:

`\sqrt[3]{(9r)/(2)}=(1)/(2)r`

`\left(\sqrt[3]{(9r)/(2)}\right)^3=\left((1)/(2)r\right)^3`

`(9r)/(2)=16r^3`

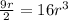
Dividing both sides of the equation by 9r, we get:

`(1)/(2)=(16r^2)/(9)`

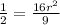
Multiplying both sides of the equation by 9, we get:

`(9)/(2)=16r^2`

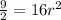
Dividing both sides of the equation by 16, we get:

`(9)/(32)=r^2`

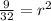
Taking the square root of both sides of the equation, we get:

`\pm\sqrt{(9)/(32)}=r`

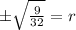
Since r cannot be negative, we can eliminate the negative square root. Therefore, the value of r is **1**.

The diagram shows that the equation
`$\sqrt[3]{(9r)/(2)}=(1)/(2)r$` can be interpreted as a cubic function.

The graph of the cubic function intersects the x-axis at three points, but only one of those points is positive.

Therefore, the only positive solution to the equation is r = 1.