Question

This question has two parts. First, answer Part A. Then, answer Part B.

Part A
Fill in the blank question.
PURCHASING A supermarket chain closely monitors how many bottles of sunscreen it sells each year so that it can reasonably predict how many bottles to stock in the following year. Let x be the number of years since 2010.



Year 2013 2014 2015 2016 2017
Bottles of Sunscreen 60,200 65,000 66,300 65,200 70,600


a. Find the equation for the best-fit line for the data. Round to the nearest hundredth, if necessary.



y =
x +

Answer 1

1. The equation for the best-fit line is y = 4800x - 378400, where y is the number of bottles of sunscreen sold and x is the number of years since 2010.

2. The supermarket can expect to sell approximately 24,000 bottles of sunscreen in 2025.

1.

Gather the data: The data points in the table are: (2013, 60200), (2014, 65000), (2015, 66300), (2016, 65200), and (2017, 70600).

Calculate the slope: Use the formula for the slope,

m =
`((y_2 - y_1))/((x_2 - x_1))`

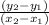
where
`(x_1, y_1)` and
`(x_2, y_2)` are two data points.

Choose any two data points from the table. For example, using the points (2013, 60200) and (2014, 65000), the slope,

m =
`((65000 - 60200))/((2014 - 2013))` = 4800 bottles/year.

Calculate the y-intercept: Use the formula for the y-intercept,

b =
`y_1 - mx_1`

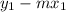
where
`(x_1, y_1)` is any data point and m is the slope calculated

Using the same point (2013, 60200) and the slope m = 4800, the y-intercept,

b = 60200 - (4800)(2013) = -378400.

Write the equation: The equation of the best-fit line is therefore

y = mx + b

where m = 4800 and b = -378400.

In this case, the equation is y = 4800x - 378400.

2.

Use the equation: Plug x = 15 (since 2025 is 15 years after 2010) into the equation

y = 4800x - 378400.

Calculate the predicted value:

y = (4800)(15) - 378400 = 24000.