The solution is x = -1 and y = -5 for the system 4x - y = 1 and -4x - 6y = 34.
To solve the system of equations 4x - y = 1 and -4x - 6y = 34, we'll use either the substitution or elimination method. Let's use the elimination method to solve this system by eliminating one of the variables.
First, let's multiply the first equation by 6 to make the coefficients of y in both equations equal:
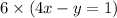
24x - 6y = 6
Now, rewrite the second equation:
-4x - 6y = 34
Let's add these equations together to eliminate y:
(24x - 6y) + (-4x - 6y) = 6 + 34
24x - 6y - 4x - 6y = 40
20x - 12y = 40
Divide both sides of the equation by 4 to simplify:
5x - 3y = 10 [Equation A]
Now, let's return to the original equation 4x - y = 1 and rearrange it to solve for y:
y = 4x - 1 [Equation B]
Substitute Equation B into Equation A:
5x - 3(4x - 1) = 10
5x - 12x + 3 = 10
-7x + 3 = 10
-7x = 7
x = -1
Now that we've found x = -1, substitute it into Equation B to find y:
y = 4(-1) - 1
y = -4 - 1
y = -5
Therefore, the solution to the system of equations is x = -1 and y = -5.
Question:
Solve the system of equations: 4x - y = 1 and -4x - 6y = 34 to find the values of x and y.