(1) The speed of blood flow within the plaque region is approximately
 . (2) The pressure drop within the plaque region is approximately
. (2) The pressure drop within the plaque region is approximately
 .
.
(1) Speed of Blood Flow within the Plaque Region:
Given:
- Initial diameter
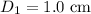
- Speed of blood flow before plaque buildup
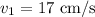
- Reduced diameter within the plaque region
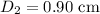
Using the continuity equation,
 , where
, where
 :
:
![\[v_2 = (A_1)/(A_2)v_1\]](https://img.qammunity.org/2024/formulas/mathematics/college/r0gmw3d5n6gj2ecv7xpur096xw9m1888n7.png)
Substitute the values:
![\[v_2 = ((\pi (1.0)^2)/(4))/((\pi (0.90)^2)/(4)) * 17 \approx (1.0)/(0.81) * 17 \approx 21.0 \ \text{cm/s}\]](https://img.qammunity.org/2024/formulas/mathematics/college/p4vy9lb9hki8z8hahwr8jdemhzz4gengao.png)
(2) Pressure Drop within the Plaque Region:
Using Bernoulli's equation:
![\[P_1 + (1)/(2)\rho v_1^2 = P_2 + (1)/(2)\rho v_2^2\]](https://img.qammunity.org/2024/formulas/mathematics/college/y5kg9zv5yo6qdvs0i4vqrvinr76ai1uqav.png)
The pressure drop
 is given by
is given by
 .
.
Substitute the values:
![\[\Delta P = (1)/(2)\rho(v_2^2 - v_1^2) = (1)/(2) * 1060 \left((21.0)^2 - (17)^2\right) \approx 2122 \ \text{Pa} \approx 21.2 \ \text{kPa}\]](https://img.qammunity.org/2024/formulas/mathematics/college/sgd8aivi1g0whnjqegscz0e4qihuq02gk9.png)
The complete question is:
(attached)