The correct answer is D.
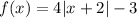
To solve this problem, we can use the following steps:
1. Identify the vertex of the graph. The vertex of the graph is $(-2,-3)$.
2. Identify whether the graph opens up or down. The graph opens downward.
3. Identify whether the graph is stretched or compressed vertically. The graph is stretched vertically by a factor of 4.
4. Identify whether the graph is shifted horizontally or vertically. The graph is shifted to the left by 2 units.
Based on this information, we can write the following general form for the absolute value function:
f(x) = a|x - h| + k
where $(h,k)$ is the vertex of the graph and $a$ is the vertical stretch factor.
Since the graph opens downward, we know that $a$ is negative. Since the graph is stretched vertically by a factor of 4, we know that $a=-4$. Since the graph is shifted to the left by 2 units, we know that $h=-2$. Since the vertex of the graph is $(-2,-3)$, we know that $k=-3$.
Substituting these values into the general form, we get the following function:
f(x) = -4|x + 2| - 3
Therefore, the correct answer is D
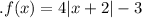
Absolute value functions are functions that take the distance from an input value to zero as their output. The general form of an absolute value function is:
f(x) = a|x - h| + k
where:
$a$ is the vertical stretch factor
$h$ is the horizontal shift
$k$ is the vertical shift
The vertex of the graph of an absolute value function is always at the point $(h,k)$.
In the graph you provided, the vertex of the graph is $(-2,-3)$. This means that the function is shifted to the left by 2 units and down by 3 units.
The graph also opens downward, which means that the vertical stretch factor is negative. Since the graph is stretched vertically by a factor of 4, the vertical stretch factor is $-4$.
Therefore, the correct absolute value function for the graph is:
f(x) = -4|x + 2| - 3
This function can also be written as:
f(x) = -4|x - (-2)| - 3
This is because the absolute value of $x - (-2)$ is the same as the absolute value of $x + 2$.
Here is a table showing the different values of $x$ and the corresponding values of $f(x)$:
| x | f(x) |
| -4 | 5 |
| -3 | 3 |
| -2 | -3 |
| -1 | 5 |
| 0 | 7 |
| 1 | 9 |
| 2 | 11 |
| 3 | 13 |
As you can see, the function decreases as $x$ increases from the left of the vertex, and increases as $x$ increases from the right of the vertex.