The efficient level of consumption in period 1 is
 units.
units.
To find the efficient level of consumption in period 1, we need to compare the marginal benefit of consumption (given by the inverse demand curve) with the marginal cost of extraction.
The total benefit from consuming in period 1 is the area under the demand curve up to the quantity consumed. The total cost is the quantity consumed times the constant marginal cost of $5.
The inverse demand in period 1 is given by
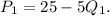
The total benefit (TB) is the integral of this demand function:
TB=
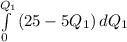
TB=
![[25 Q_1- (5)/(2)Q(2)/(1) ]^(Q_1) _0](https://img.qammunity.org/2024/formulas/mathematics/college/dqyteg1wt21luh4y2ccslw1bmd8aq63nyt.png)
TB=25
 −
−
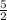 Q
Q
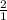
Now, the social planner maximizes the net benefit, which is the total benefit minus the total cost:
NB=TB−TC
NB=(25Q_1 −
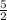 Q
Q
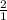 )−5Q_1
)−5Q_1
NB=20
 −
−
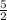 Q
Q
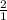
To find the efficient level of consumption, we need to find the quantity that maximizes net benefit. Take the derivative of the net benefit with respect to Q_1 and set it equal to zero:
 =
=
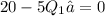
Solving for Q_1:

So, the efficient level of consumption in period 1 is
 units.
units.