Question

In an economy of 1,000 people each person has the utility function for two goods X and Y. Let good Y be the numeraire good (you can think of it as money), with pY = 1, and p X be the price of good X. Each consumer has income I = 4.

Answer 1

The optimal consumption bundle for each consumer is to spend half of their income on good X (X=2) and the other half on the numeraire good Y (Y=2). The equilibrium price of good X in the market is pX =2.

To find the optimal consumption bundle for each consumer and the equilibrium price of good X in the market, we can use the concept of consumer choice and market equilibrium in microeconomics.

Each consumer aims to maximize utility subject to the budget constraint, expressed as:

U(X,Y)=X⋅Y

The budget constraint is given by:

I=pX⋅ X +p ⋅Y

Given that I=4,pY =1, and pX is the price of good X, we substitute these values into the budget constraint:

4=pX ⋅X+Y

Since pY=1, we can simplify the equation to 4=pX ⋅X+Y.

Now, to find the optimal consumption bundle, we need to differentiate the utility function with respect to X and set it equal to the marginal rate of substitution (MRS):

MRS=
`MU _(X)`​/
`MU_(Y)`

=
`(px)/(1)`

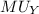
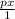
This gives us the condition X=pX .

Substituting this into the budget constraint, we get 4=2⋅pX , which yields pX =2.

Therefore, the optimal consumption bundle for each consumer is to spend half of their income on good X (X=2) and the other half on the numeraire good Y (Y=2).

The equilibrium price of good X in the market is pX =2.

Question

In an economy of 1,000 people each person has the utility function for two goods X and Y. Let good Y be the numeraire good (you can think of it as money), with pY = 1, and p X be the price of good X. Each consumer has income I = 4. Find the optimal consumption bundle for each consumer, given the prices and income. Determine the equilibrium price of good X in the market.