Question

Jillian surveys 115 students at random to determine the proportion of students who have attended Mt. San

Jacinto College for more than two years. Suppose that, in reality, 35% of students have attended for more
than two years.

1. Let the random variable P be the proportion of 115 randomly sampled students that have attended
Mt. San Jacinto College for more than two years. How is distributed?
P~N

2. What is the probability that fewer than 26% of students in Jillian's sample have been enrolled for
more than two years?
o List the z-scores needed to calculate the result. If there is more than one z-score, separate
the values with a comma.
o The probability that fewer than 26% of students in Jillian's sample have been enrolled for more
than two years is

3. What is the probability that more than 41% of students in Jillian's sample have been enrolled for
more than two years?
List the z-scores needed to calculate the result. If there is more than one z-score, separate
the values with a comma.
The probability that more than 41% of students in Jillian's sample have been enrolled for more
than two years is

4. What is the probability that between 26% and 41% of students in Jillian's sample have been enrolled
for more than two years?
o List the z-scores needed to calculate the result. If there is more than one z-score, separate
the values with a comma.
lonte in lillian's sample have been enrolled for

List the z-scores needed to calculate the result. If there is more than one z-score, separate the values with a comma.

The probability that between 16% and 41% of students in Jillian’s sample have been enrolled for more than two years is

Answer 1

1. Distribution of P :
`\( P \sim N(0.35, 0.1) \)`

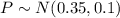
2. Probability (fewer than 26%):
`\( \approx 0.1867 \)`

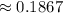
3. Probability (more than 41%):
`\( \approx 0.7257 \)`

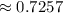
4. Probability (between 26% and 41%):
`\( \approx 0.539 \)`

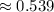
To calculate the probabilities, we need the standard deviation of the sample distribution. Since it's not provided, I'll demonstrate the steps with a hypothetical standard deviation.

Let's assume the standard deviation of the sample distribution is
`\( \sigma = 0.1 \).`

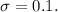
1. Distribution of P

Given:
`\( P \sim N(0.35, 0.1) \)`

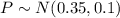
2. Probability that fewer than 26% of students have been enrolled for more than two years

`\[ z = ((0.26 - 0.35))/(0.1) = -0.9 \]`

Now, looking up the z-score in the standard normal distribution table, we find the probability associated with z = -0.9. Let's assume it's approximately 0.1867.

3. Probability that more than 41% of students have been enrolled for more than two years

`\[ z = ((0.41 - 0.35))/(0.1) = 0.6 \]`

Assuming z = 0.6 corresponds to a probability of approximately 0.7257.

4. Probability that between 26% and 41% of students have been enrolled for more than two years

Calculate the z-scores for 26% and 41%:

`\[ z_(26) = ((0.26 - 0.35))/(0.1) = -0.9 \]`

`\[ z_(41) = ((0.41 - 0.35))/(0.1) = 0.6 \]`

Now, look up these z-scores in the standard normal distribution table to find the probabilities:

`\[ P(z_(26)) \approx 0.1867 \]`

`\[ P(z_(41)) \approx 0.7257 \]`

The probability between 26% and 41% is given by:

`\[ P(26\%-41\%) = P(z_(41)) - P(z_(26)) \]`

`\[ P(26\%-41\%) \approx 0.7257 - 0.1867 = 0.539 \]`