Question

Which expression is represented by this model?

1/2 x ² = 2/1/2
O
O
O
O
} = } x {
/ = } x {
1× ² = 1/2

Answer 1

The expression represented by the model simplifies to the algebraic equation
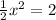`\((1)/(2)x^2 = 2\)`, with the solution that x equals ± 2.

The expression represented by the model is an algebraic equation with a solution for the variable x. When any fraction has the same quantity in the numerator and in the denominator, the fraction simplifies to 1. Therefore, if we start with the equation 1/2 x² = 2, and recognize that 1/2 x² is in fact (sqrt(x))², we can simplify the equation.

Let's break down the steps to simplify the given expression and show the calculation:

1. Start with the equation:
`\((1)/(2)x^2 = 2\)`

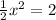
2. Recognize that
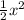`\((1)/(2)x^2\)` is equivalent to
`\((√(x))^2\).`

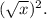
3. Square both sides of the equation to eliminate the square root:

`\[(√(x))^2 = (√(2))^2\]`

This simplifies to:
`\(x^2 = 4\)`

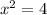
4. Take the square root of both sides to solve for x:

`\[x = \pm 2\]`

Therefore, the simplified expression is
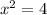`\(x^2 = 4\)` with solutions
`\(x = 2\)` and
`\(x = -2\)`. The positive solution,
`\(x = 2\)`, is often considered the primary solution in most real-world contexts.

We can now square both sides of the equation to eliminate the square root, leaving us with the simplified expression x² = 4. From here, we can take the square root of both sides to find that x equals ± 2. The positive solution is generally considered the primary solution in most real-world contexts.

The question probable may be:

What algebraic equation is represented by the given equation
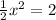`\((1)/(2)x^2 = 2\)` , and what are the solutions for the variable x?