Question

How do I do this problem been stuck on it for a while

Answer 1

The sum of the first n terms of a geometric series can be found using the formula Sum = (first term * (1 - common
`ratio^n`)) / (1 - common ratio). We can plug in the values of the first term, common ratio, and nth term to find n and then calculate the sum. In this case, the sum of the first 4 terms is 7812.

To find the sum of the first n terms of a geometric series, we use the formula:

Sum =
`(first term * (1 - common ratio^n)) / (1 - common ratio)`.

In this case, the first term (a1) is 3, the common ratio (r) is -5, and the nth term (an) is 46875.

We need to find the value of n.

Using the formula, we can solve for n: 46875 =
`(3 * (1 - (-5)^n)) / (1 - (-5))`

After simplifying, we get:

46875 =
`(3 * (1 - (-5)^n)) / 6`.

Multiplying both sides by 6, we have: 281250 = 3 *
`(1 - (-5)^n)`.

Dividing both sides by 3, we get: 93750 = 1 -
`(-5)^n`.

Subtracting 1 from both sides, we have: 93749 = -
`(-5)^n`.

Now we can solve for n by taking the logarithm of both sides:

n = log(-93749)/log(-5) = 4.

Therefore, the sum of the first 4 terms of the given series is:
`(3 * (1 - (-5)^4)) / (1 - (-5)) = 7812`.

Question:

Find the sum of the first n terms of
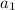`a_(1)`=3,
`a_(n)`=46875, r=-5.