Question

What is the mean free path in m of a gas of randomly-moving hard spheres of radius 0.1 × 10-9 m when the number density of spheres is 2.5 × 1019 per cubic meter?

Answer 1

The mean free path of a gas of randomly-moving hard spheres with a given radius and number density can be calculated using the formula mean free path =
`1 / (√(2) * \pi * (radius^2) * number density)`. Applying this formula to the given values, the mean free path is found to be 2.56 x
`10^-9` m.

The mean free path of a gas of randomly-moving hard spheres can be calculated using the formula:

mean free path =
`1 / (√(2) * \pi * (radius^2) * number density)`

Using the given values:

Radius = 0.1 ×
`10^-^9` m

Number density = 2.5 ×
`10^1^9` per cubic meter

Substituting these values, we can find the mean free path to be:

mean free path =
`1 / (√(2) * \pi * (0.1 * 10^-^9)^2 * 2.5 * 10^1^9)`

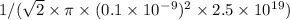
Simplifying the expression:

mean free path = 2.56 ×
`10^-^9` m