As we get
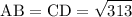 and
and
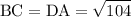 it is proven that a given quadrilateral is a parallelogram.
it is proven that a given quadrilateral is a parallelogram.
Let A, B, C and D is a quadrilateral.
It have a coordinates as follows:
Point A = (-7,-3)
Point B = (5,10)
Point C = (15,8)
Point D = (3,-5)
Here we have to use the distance formula
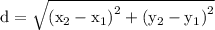
By substituting the values here,
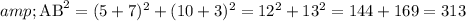
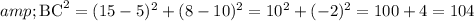
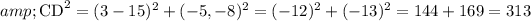
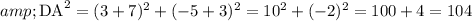
So,
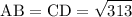 and
and
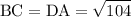
i.e., The opposite sides are equal. Hence ABCD is a parallelogram.