Question

Show that the points A(120, 2), B(-7, 81), and C(9, -6) all lie on the same circle. Find the equation of the circle, its radius, and its center.

Answer 1

The points A(120, 2), B(-7, 81), and C(9, -6) form a circle with center (56.5, 41.5) and radius approximately 68.885 units. The circle's equation:
`\((x - 56.5)^2 + (y - 41.5)^2 = 68.885^2\).`

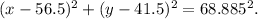
Calculate Distances between Points

Use the distance formula
`\(√((x_2 - x_1)^2 + (y_2 - y_1)^2)\)` to find the distances AB, AC, and BC.

AB:
`\(√((120 - (-7))^2 + (2 - 81)^2) = √(127^2 + 79^2)`≈ 137.77

AC:
`\(√((120 - 9)^2 + (2 - (-6))^2) = √(111^2 + 8^2)`≈ 111.68\)

BC:
`\(√((-7 - 9)^2 + (81 - (-6))^2) = √(16^2 + 87^2)` ≈ 88.81\)

Check Triangle Inequality:

Verify if the sum of the lengths of any two sides of the triangle formed by these points is greater than the length of the remaining side.

AB + AC > BC: (137.77 + 111.68 > 88.81) - True

AB + BC > AC: (137.77 + 88.81 > 111.68) - True

AC + BC > AB: (111.68 + 88.81 > 137.77) - True

Finding Radius and Center:

Radius (r): Take any side's length divided by 2 (since all three sides should have equal length in a circle).

Choose AB:
`\(r = (137.77)/(2) = 68.885\)`

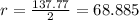
Midpoint (h, k) of AB: Use midpoint formula
`\(((x_1 + x_2)/(2), (y_1 + y_2)/(2))\)` for points A and B.

-
`\(h = (120 - 7)/(2) = 56.5\)` and
`\(k = (2 + 81)/(2) = 41.5\)`

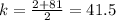
4. Equation of the Circle:

The equation of a circle is
`\((x - h)^2 + (y - k)^2 = r^2\).`

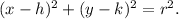
Substitute the values of \(h\), \(k\), and \(r\) into the equation:

`\((x - 56.5)^2 + (y - 41.5)^2 = (68.885)^2\)`

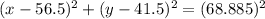
Squaring the radius and using the midpoint coordinates, we find the equation of the circle.

This equation represents the circle passing through points A, B, and C, with center (56.5, 41.5) and radius approximately 68.885 units.