Question

A research scholar wants to know how many times per hour a certain strand of virus reproduces. The mean is found to be 12.9 reproductions and the population standard deviation is known to be 2.2. If a sample of 358 was used for the study, construct the 90% confidence interval for the true mean number of reproductions per hour for the virus. Round your answers to one decimal place.

Answer 1

The 90% confidence interval for the mean is 12.6 to 13.2 reproductions per hour.

We are interested in constructing a 90% confidence interval for the mean number of virus reproductions. We know the population standard deviation is σ=2.2 reproductions per hour, and we have a sample size of n=358.

The margin of error is found with the formula E=
`Z^** (\sigma)/(√(n) )`

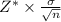
The confidence level is 90%, so we find the corresponding z-score using the normalcdf function on most calculators. The output is 1.645.

The margin of error is then

E = 1.645⋅
`(2.2)/(√(358) )`

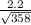
E = 0.30 reproductions per hour.

The mean number of reproductions per hour is μ=12.9, so the 90% confidence interval is μ ± E = 12.9 ± 0.30 = (12.60,13.20) reproductions per hour.