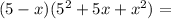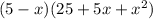Question

How do you factor 125-x^3?

Answer 1

First Image is the answer the second is the steps

Best of Luck

Answer 2

Explanation:

We have

`125 - x {}^(3)`

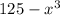
First, 125 is a perfect cube because

`5 * 5 * 5 = 125`

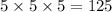
and

x^3 is a perfect cube because

`x * x * x = x {}^(3)`

so we can use the difference of cubes identity

`( {x}^(3) - {y}^(3) ) = (x - y)( {x}^(2) + xy + {y}^(2) )`

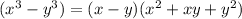
Let say we have two perfect cubes:

64 because 8×8×8=64

and 27 because 3×3×3=27 and let subtract

`64 - 27`

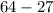
we know that

`64 - 27 = 37`

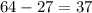
but using the difference of cubes identity we should get the same thing.

Remeber cube root of 64 is 4 and cube root of 27 is 3 so we have

`(4 - 3)( {4}^(2) + 4(3) + 3 {}^(2) )`

`1(16 + 12 + 9) = 1(37) = 37`

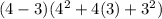
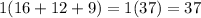
So the difference of cubes works for real numbers. This is a good way to help remeber the identity using real numbers.

Back on to the topic,

we know that 5 is cube root of 125 and x is the cube root of x^3 so we have

`(5 - x)( {5}^(2) + 5x + {x}^(2) ) =`

`(5 - x)(25 + 5x + {x}^(2) )`