Question

Evaluate the surface integralstudent submitted image, transcription available belowS F · dS for the given vector field F and the oriented surface S. In other words, find the flux of F across S. For closed surfaces, use the positive (outward) orientation. F(x, y, z) = xy i + 12x2 j + yz k S is the surface z = xey, 0 ? x ? 1, 0 ? y ? 3, with upward orientation

Answer 1

To evaluate the surface integral, find the flux of the vector field F across the surface S with the given orientation. So, the final answer, the surface integral (flux) of F over the surface S, is 0

Step-by-step explanation:

To evaluate the surface integral, we need to find the flux of the vector field F = xy i + 12x^2 j + yz k across the surface S: z = xey with upward orientation.

1. First, find the unit normal vector to the surface by taking the gradient of the surface equation: n = (∇z)/|∇z| = yey i + (1 + xy)j + xey k.
2. Next, calculate the dot product of the vector field F and the unit normal vector n: F · n = (xy)(yey) + (12x^2)(1 + xy) + (yz)(xey).
3. Finally, integrate the dot product over the surface S to calculate the flux: ∫∫ (F · n) dS.
4. Integrate the Dot Product over the Surface: Now that our integrand is 0, the integral is straightforward:

`\( \iint_S F \cdot dS = \int_0^1 \int_0^3 0 \, dy \, dx = 0 \)`

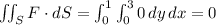
So, the final answer, the surface integral (flux) of F over the surface S, is 0.