The 80% confidence interval for the mean noise level is approximately (127.26, 141.943) decibels.
How did we get the value?
To construct an 80% confidence interval for the mean noise level, we can use the t-distribution since the sample size is small (n < 30). Here are the steps:
1. Calculate the sample mean (x-bar):
x-bar =
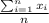
2. Calculate the sample standard deviation (s):
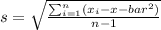
3. Determine the t-value for an 80% confidence interval with
 degrees of freedom.
degrees of freedom.
You can find this value from a t-distribution table or use statistical software.
4. Calculate the margin of error (ME):
![\[ ME = t * \left( (s)/(√(n)) \right) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/mq5xed7jcqdt7fyd3bwyffxpv2ihvtg7za.png)
5. Construct the confidence interval:
![\[ \text{Confidence Interval} = ({x-bar} - ME, {x-bar} + ME) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/vnp335qfpns7b54zoe3qsyxbzw2z5kpeio.png)
Let's go through the calculations:
Data: 132, 126, 135, 147, 133
n = 5
1. Calculate the sample mean (x-bar):
![\[ \bar{x} = (132 + 126 + 135 + 147 + 133)/(5) = (673)/(5) = 134.6 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/an3pt09oyjlke9jjizbvp5ywd5if94hgqy.png)
2. Calculate the sample standard deviation (s):
![\[ s = \sqrt{((132-134.6)^2 + (126-134.6)^2 + (135-134.6)^2 + (147-134.6)^2 + (133-134.6)^2)/(4)} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ml5ddr09mhcspx74hac680zqnscd40rgri.png)
![\[ s \approx \sqrt{(6.76 + 73.96 + 0.16 + 153.76 + 2.56)/(4)} \approx \sqrt{(237.2)/(4)} \approx √(59.3) \approx 7.70 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/wis2w47rpf23kqrhxjs1njlw07c70fyvjp.png)
3. Determine the t-value for an 80% confidence interval with 4 degrees of freedom.
Using a t-distribution table, df = 4, the t-value is approximately 2.132.
4. Calculate the margin of error (ME):
![\[ ME = 2.132 * \left( (7.70)/(√(5)) \right) \approx 2.132 * \left( (7.70)/(√(5)) \right) \approx 2.132 * 3.444 \approx 7.343 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/e2q03dmq97f76eev1lsifxlc468r9l3kdj.png)
5. Construct the confidence interval:
![\[ \text{Confidence Interval} = (134.6 - 7.343, 134.6 + 7.343) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/7z6cndpdjg8hj7fqgs99cqwyr450k48qhs.png)
![\[ \text{Confidence Interval} \approx (127.26, 141.943) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/8rqwpkxcyv5xvhbq59w7550snxxql3bd9u.png)
So, the 80% confidence interval for the mean noise level is approximately (127.26, 141.943) decibels.