Question

Noise levels at 5 airports were measured in decibels yielding the following data:

132,126,135,147,133

construct the 80% confidence interval for the mean noise level at such locations. assume the population is approximately normal.

Answer 1

The 80% confidence interval for the mean noise level is approximately (127.26, 141.943) decibels.

How did we get the value?

To construct an 80% confidence interval for the mean noise level, we can use the t-distribution since the sample size is small (n < 30). Here are the steps:

1. Calculate the sample mean (x-bar):

x-bar =
`(\sum_(i=1)^(n) x_i)/(n)`

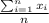
2. Calculate the sample standard deviation (s):

`\[ s = \sqrt{(\sum_(i=1)^(n) (x_i - x-bar^2))/(n-1)`

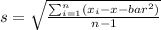
3. Determine the t-value for an 80% confidence interval with
`\(n-1\)` degrees of freedom.

You can find this value from a t-distribution table or use statistical software.

4. Calculate the margin of error (ME):

`\[ ME = t * \left( (s)/(√(n)) \right) \]`

5. Construct the confidence interval:

`\[ \text{Confidence Interval} = ({x-bar} - ME, {x-bar} + ME) \]`

Let's go through the calculations:

Data: 132, 126, 135, 147, 133

n = 5

1. Calculate the sample mean (x-bar):

`\[ \bar{x} = (132 + 126 + 135 + 147 + 133)/(5) = (673)/(5) = 134.6 \]`

2. Calculate the sample standard deviation (s):

`\[ s = \sqrt{((132-134.6)^2 + (126-134.6)^2 + (135-134.6)^2 + (147-134.6)^2 + (133-134.6)^2)/(4)} \]`

`\[ s \approx \sqrt{(6.76 + 73.96 + 0.16 + 153.76 + 2.56)/(4)} \approx \sqrt{(237.2)/(4)} \approx √(59.3) \approx 7.70 \]`

3. Determine the t-value for an 80% confidence interval with 4 degrees of freedom.

Using a t-distribution table, df = 4, the t-value is approximately 2.132.

4. Calculate the margin of error (ME):

`\[ ME = 2.132 * \left( (7.70)/(√(5)) \right) \approx 2.132 * \left( (7.70)/(√(5)) \right) \approx 2.132 * 3.444 \approx 7.343 \]`

5. Construct the confidence interval:

`\[ \text{Confidence Interval} = (134.6 - 7.343, 134.6 + 7.343) \]`

`\[ \text{Confidence Interval} \approx (127.26, 141.943) \]`

So, the 80% confidence interval for the mean noise level is approximately (127.26, 141.943) decibels.