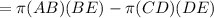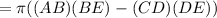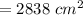Question

The radii of the top and bottom of a bucket are 21cm and 14 cm. Determine the capacity and curved surface area of the bucket if its height is 24cm.

Answer 1

Explanation:

Given:

AB = 21 cm

CD = 14 cm

AC = 24 cm

Based on Triangle Proportionality Theorem:

AB : CD = AE : CE

AB : CD = (CE + AC) : CE

21 : 14 = (CE + 24) : CE

21CE = 14(CE + 24)

21CE - 14CE = 336

CE = 336 ÷ 7

= 48 cm

Capacity of bucket = V. big cone (ABE) - V. small cone (CDE)

`=(1)/(3) \pi AB^2(AE)-(1)/(3) \pi CD^2(CE)`

`=(1)/(3) \pi (AB^2(AE)-CD^2(CE))`

`=(1)/(3) ((22)/(7)) ((21)^2(24+48)-(14)^2(48))`

`=23408\ cm^3`

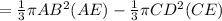
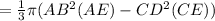
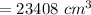
BE² = AB² + AE²

= 21² + 72²

= 5625

BE = 75 cm

DE² = CD² + CE²

= 14² + 48²

= 2500

DE = 50 cm

Curved surface = surface of big cone (ABE) - surface of small cone (CDE)

`=\pi(AB)(BE) - \pi (CD)(DE)`

`=\pi((AB)(BE) - (CD)(DE))`

`=(22)/(7) ((21)(75)-(14)(48))`

`=2838\ cm^2`