Question

I need a minimal of 3 paragraphs explain how the problem was solved and if it’s correct, please help!

Answer 1

That is a question about spatial geometry.

In our problem, we have to calculate lateral surface area of a triangular prism. Let's see how to solve this.

A triangular prism has 5 faces: 3 equals rectangles and 2 equals triangles. If we can find a way to calculate those areas, we can solve the problem.

The first thing that we should note is that we know the dimensions of the rectangular faces. The dimesions of the rectangular are 5cm and 8cm. To calculate the are of a rectangle, we multiplicate the dimensios of it. Therefore, each rectangle (in our problem) has
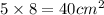`5 * 8 = 40cm^2` of area. There are 3 rectangles, so, the sum of the 3 rectangular area is
`40 + 40 + 40 = 120cm^2`.

Now, we need to know the area of the triangular areas. To calculate the area of a triangle, we need to know the value of the base and the value of the height.

In the image, we know the value of the base, but we do not know the value of the height. To calculate the height, we can use the Pythagorean Theorem because we have a right triangle. (Please find attached the document.)

The Pythagorean theorem says that:

`\boxed{a^2 = b^2 + c^2}`

a is the hypotenuse and b and c are cathetus.

In this right triangle, the value of the hypotenuse is 5cm and the value of one cathetus is the half of 6cm (that is 3cm). Let's replace the values in the expression:

`a^2=b^2+c^2\\5^2= 3^2 +c^2\\25 = 9 + c^2\\c^2 = 25 - 9\\c^2 = 16\\c = √(16) \\c = 4cm`

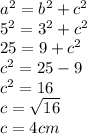
Now, we know the bases and the height of the triangular areas. To calculate the area of a triangle, we multiply the base and the height and we divided the result by 2. See the expression:

`\boxed{A_t=\frac{b* h} {2}}`

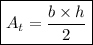
b is the base and h is the height. Let's replace the values in the expression:

`A_t = (b* h)/(2) \\A_t = (6*4)/(2) \\A_t = (24)/(2) \\A_t = 12cm^2`

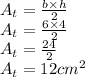
So, each triangular area has 12cm² of area. Therefore, the sum of the triangular areas is
`12 + 12 = 24cm^2`.

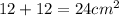Finally, we know that the sum of the rectangular area is 120cm², and the sum of the triangular area is 24cm², so, the lateral surface area is
`120 + 24 = 144cm^2`.

In other words, they didn't choose the correct answer because the correct answer is J) 144 cm².

I hope I've helped. :D

Enjoy your studies. \o/