1 Answer

Sirpadk · Answer 1 · 2022-05-28T14:00:33+0000

Given:

One midsegment of an equilateral triangle.

To find:

The ratio of the length of one midsegment of an equilateral triangle to the sum of two of its side lengths.

Solution:

All sides of an equilateral triangle are same.

Let a be the each side of the equilateral triangle.

Length of the midsegment is equal to the half of the non included side or third side.

Midsegment=(a)/(2)

The sum of two side is

a+a=2a

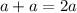
Now, the ratio of the length of one midsegment of an equilateral triangle to the sum of two of its side lengths is

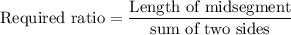
$\text{Required ratio}=\frac{\text{Length of midsegment}}{\text{sum of two sides}}$

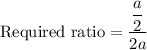
$\text{Required ratio}=((a)/(2))/(2a)$

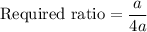
$\text{Required ratio}=(a)/(4a)$

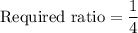
$\text{Required ratio}=(1)/(4)$

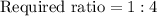
$\text{Required ratio}=1:4$

Therefore, the ratio of the length of one midsegment of an equilateral triangle to the sum of two of its side lengths is 1:4.

Please log in or register to add a comment.