Question

Next

Strontium 90 is a radioactive isotope that decays according to the eqaution A,
=
Age-0.0244
where Ao is the initial amount present and A, is the amount present after t years. If you
begin with 400 grams of strontium 90,
(a) How much strontium 90 will be left after 10 years? Round your answer to the nearest tenth
of a gram.
grams
(b) When will 170 grams of strontium 90 be left? Round your answer to the nearest tenth of a
year.
years

Answer 1

(a) 313.4 grams

(b) 35.1 years

Explanation:

Strontium 90 is a radioactive isotope that decays according to the given equation:

`\large\text{$A_t=A_0\cdot e^(-0.0244t)$}`

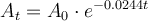
where:

• 
  `A_0` is the initial amount present.
• 
  `A_t` is the amount present after t years.

Given that that the initial amount of strontium 90 is 400 grams, we can substitute A₀= 400 into the given equation:

`\large\text{$A_t=400\cdot e^(-0.0244t)$}`

`\hrulefill`

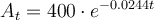
Part (a)

To determine how much strontium 90 will be left after 10 years, we can substitute t = 10 into the given equation:

`A_(10)=400\cdot e^(-0.0244(10))`

`A_(10)=400\cdot e^(-0.244)`

`A_(10)=400\cdot 0.783487634...`

`A_(10)=313.3950537...`

`A_(10)=313.4\; \rm g\;(nearest\;tenth)`

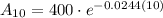
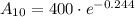
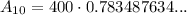
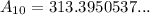
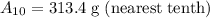
Therefore, there will be 313.4 grams of strontium 90 left after 10 years.

`\hrulefill`

Part (b)

To determine when 170 grams of strontium 90 will be left, we can substitute
`A_t = 170` into the equation and solve for t:

`170=400\cdot e^(-0.0244t)`

`(170)/(400)= e^(-0.0244t)`

`(17)/(40)= e^(-0.0244t)`

`e^(-0.0244t)=(17)/(40)`

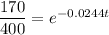
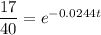
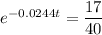
Take natural logs of both sides of the equation:

`\ln \left(e^(-0.0244t)\right)=\ln \left((17)/(40)\right)`

Apply the log power rule to the left side of the equation:

`-0.0244t\ln \left(e\right)=\ln \left((17)/(40)\right)`

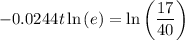
As ln(e) = 1, then:

`-0.0244t=\ln \left((17)/(40)\right)`

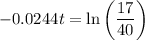
Divide both sides by -0.0244:

`t=(\ln \left((17)/(40)\right))/(-0.0244)`

`t=35.068283199...`

`t=35.1\; \rm years\;(nearest\;tenth)`

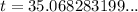
Therefore, there will be 170 grams of strontium 90 left after 35.1 years.