Question

A Telecom service provider claims that individual customers pay on a mean 400$ per month with standard deviation of 25S. A random sample of 50 customers bills during a given month is taken with a mean of 250S and standard deviation of 15$. What to say with respect to the claim made by the service provider? Carry out an appropriate hypothesis test for the validity of Telecom service provider's claim at a = 0.05.

Answer 1

The validity of the Telecom service provider's claim, a hypothesis test is conducted using a t-test with a sample mean of 250, a sample standard deviation of 15, a sample size of 50, and a population standard deviation of 25. The calculated t-statistic is approximately -10.53, which is greater than the critical t-value of 2.009. Therefore, the null hypothesis is rejected, and there is sufficient evidence to suggest that the mean bill per month for individual customers is significantly lower than 400.

The validity of the Telecom service provider's claim, we can perform a hypothesis test. Let's define the null and alternative hypotheses:

• Null hypothesis (H0): The mean bill per month for individual customers is 400.
• Alternative hypothesis (H1): The mean bill per month for individual customers is not 400.

Mathematically, this can be expressed as:

H0: μ = 400

H1: μ ≠ 400

Given that the sample mean
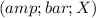`(&bar;X)` is 250, the sample standard deviation (s) is 15, the sample size (n) is 50, and the population standard deviation (σ) is 25, we can use a t-test since the population standard deviation is not known.

The test statistic for a t-test is given by:

t = (
`(&bar;X - u)/(s / √(n) ))`)

Now, let's calculate the t-statistic:

`t = (250 - 400)/((15)/(√(50) ) )`

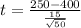
Calculating this gives us the t-statistic. Once we have the t-statistic, we can compare it to the critical t-value at a 0.05 significance level with 49 degrees of freedom (since n-1 = 50-1 = 49).

If the absolute value of the t-statistic is greater than the critical t-value, we reject the null hypothesis. Otherwise, we fail to reject the null hypothesis.

Let's proceed with the calculations:

`t ≈ -10.53`

Now, we need to compare this t-statistic to the critical t-value. The critical t-value for a two-tailed test at a 0.05 significance level with 49 degrees of freedom is approximately ± 2.009.

Since ·10.53 ≥ 2.009

∴ Reject Null Hypothesis

Conclusion: There is sufficient evidence to reject the Telecom service provider's claim that individual customers pay a mean of 400 per month. The sample data suggests a significantly lower mean bill per month.

Answer 2

To test the claim made by the Telecom service provider, use a hypothesis test. Calculate the z-score, determine the p-value, and make a conclusion based on the significance level.

Step-by-step explanation:

To test the claim made by the Telecom service provider, we can use a hypothesis test. The null hypothesis (H0) is that the mean monthly payment is $400, and the alternative hypothesis (H1) is that the mean monthly payment is not $400.

To carry out the hypothesis test, we can calculate the z-score using the formula: z = (sample mean - population mean) / (population standard deviation/sqrt (sample size)).

Based on the calculated z-score, we can determine the p-value and compare it to the significance level (0.05) to make a conclusion. If the p-value is less than 0.05, we reject the null hypothesis and conclude that there is evidence to suggest that the mean monthly payment is different from $400.