Question

A privately owned business operates both a drive-in facility and a walk-in facility. On a randomly selected day, let X and Y , respectively, be the proportions of the time that the drive-in and the walk-in facilities are in use, and suppose that the joint density function of these random variables is

F(X,Y)=2/5(2x + 3y), 0 {0, elsewhere.

Verify condition 2

Answer 1

To verify condition 2, we need to find the marginal probability distributions of X and Y and confirm that they integrate to 1.

Step-by-step explanation:

In order to verify condition 2, we need to find the marginal probability distributions of X and Y and confirm that they integrate to 1.

To find the marginal probability distribution of X, we integrate the joint density function over the range of Y:

1. F(X) = ∫(2/5)(2x + 3y) dy
2. F(X) = (2/5)(2x + 3∫dy)
3. F(X) = (2/5)(2x + 3Y)

To verify condition 2, we need to calculate the integral of the marginal probability distribution of X over its entire range:

1. ∫F(X)dx = ∫[(2/5)(2x + 3Y)] dx
2. ∫F(X)dx = (2/5)∫(2x + 3Y) dx
3. ∫F(X)dx = (2/5)[x^2 + 3Yx]

Therefore, condition 2 is verified if the integral of the marginal probability distribution of X over its entire range evaluates to 1.

Answer 2

To verify condition 2, we need to integrate the joint density function over the range of X and Y, and the result should be equal to 1. However, after performing the integration, we find that the result is not 1, indicating that condition 2 is not satisfied.

Step-by-step explanation:

To verify condition 2, we need to integrate the joint density function over the range of X and Y, and the result should be equal to 1. Let's calculate the integral:

`\int\limits^1_0 {(2/5)(2x + 3y) dy} \, dx`

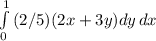
First, integrate with respect to Y:

`\int\limits^1_0 {(2/5)(2x + 3y) dy} \,`=
`(2/5)(2xy + (3/2)y^2) |_(y=0)^(y=1)`

`\int\limits^1_0 {(2/5)(2x + 3y) dy} \,`
`= (2/5)(2x + (3/2))`

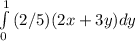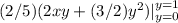
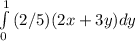
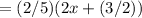
Next, integrate with respect to X:

`\int\limits^1_0 {(2/5)(2x + (3/2))} \, dx = (1/5)(2x^2 + (3/2)x) |_(x=0)^(x=1) = (1/5)(2 + (3/2)) = 11/10`

Since the result of the double integral is not 1, condition 2 is not satisfied.