Question

A local hardware store claims that the mean waiting time in line is less than 3.5 minutes. a random sample of 20 customers has a mean of 3.2 minutes with a standard deviation of 0.8 minute. if α = 0.10, test the store's claim.

Answer 1

With a test statistic of approximately -1.676 and a p-value of 0.056 (greater than the significance level of 0.10), we fail to reject the null hypothesis. There is insufficient evidence to conclude that the mean waiting time is less than 3.5 minutes.

In this scenario, you are conducting a one-sample t-test to evaluate whether there is enough evidence to reject the null hypothesis
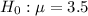`\(H_0: \mu = 3.5\)` in favor of the alternative hypothesis
`\(H_a: \mu < 3.5\)`.

Given:

- Sample mean
`(\(\bar{x}\))` = 3.2 minutes

- Sample standard deviation (s) = 0.8 minutes

- Sample size (n) = 20

- Significance level
`(\(\alpha\))` = 0.10

The test statistic (t) is calculated using the formula:

`\[ t = \frac{(\bar{x} - \mu_0)}{(s)/(√(n))} \]`

Where:

-
`\(\bar{x}\)` is the sample mean,

-
`\(\mu_0\)` is the hypothesized population mean under the null hypothesis,

- s is the sample standard deviation,

- n is the sample size.

Substitute the given values:

`\[ t = ((3.2 - 3.5))/((0.8)/(√(20))) \]`

Now, calculate the test statistic:

`\[ t = (-0.3)/((0.8)/(√(20))) \]\[ t \approx (-0.3)/((0.8)/(4.47)) \]\[ t \approx (-0.3)/(0.179) \]\[ t \approx -1.676 \]`

The degrees of freedom
`(\(df\))` for this test is
`\(n - 1 = 20 - 1 = 19\)`.

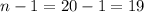Now, you need to find the p-value associated with this test statistic and degrees of freedom. Since it's a one-tailed test (less than), you'll look up the p-value for
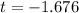`\(t = -1.676\)` with
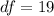`\(df = 19\)` in a t-distribution table or by using statistical software.

Assuming you find the p-value to be
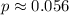`\(p \approx 0.056\)`, compare it to the significance level
`(\(\alpha\))`:

`\[ p \approx 0.056 > \alpha = 0.10 \]`

Decision:

Since the p-value is greater than the significance level, you fail to reject the null hypothesis.

Conclusion:

There is not sufficient evidence to make the conclusion that the mean waiting time at this hardware store is less than 3.5 minutes at the 0.10 significance level.

The complete question is:
A local hardware store claims that the mean waiting time in line is less than 3.5 minutes. A random sample of 20 customers has a mean of 3.2 minutes with a standard deviation of 0.8 minute. If a 0.10, test the store's claim,

H0 : μ = 3.5

Ha : μ =

Test statistic=

p-Value=

Decision=

Conclusion = There is______ sufficient evidence to make the conclusion that the mean waiting time at this hardware store is less than 3.5 minutes