Question

Find three consecutive even integers such that the product of the first and second is 8 more than 38 times the third.

Answer 1

40, 42 and 44

Explanation:

Mark these even consecutive integers as (2n-2), 2n and (2n+2)

Note that since they are integers, n > 0 and 2n is always even

Writing the equation

(2n-2) * 2n = 38 * (2n+2) + 8

// divide both sides by 2

(2n-2) * n = 19 * (2n+2) + 4

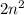`2n^(2)` - 2n = 38n + 38 + 4

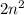`2n^(2)` - 2n - 38n - 38 - 4 = 0

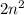`2n^(2)` - 40n - 42 = 0

// divide both sides by 2

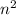`n^(2)` - 20n - 21 = 0

// rewrite the equation

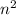`n^(2)` + n - 21n - 21 = 0

n * (n+1) - 21n - 21 = 0

n * (n+1) - 21 * (n+1) = 0

(n+1) * (n-21) = 0

// separate the two possible cases

n + 1 = 0 and n - 21 = 0

n = -1 n = 21

Note that here n has to be an integer, so case n = -1 can't be a solution. Therefore we use n = 21

Calculating the consecutive even integers

2n - 2 = 2 * 21 - 2 = 40

2n = 2 * 21 = 42

2n + 2 = 2 * 21 + 2 = 44