Question

Compare the speed of the train to the speed of the card. How much less time would it be for Lisa to travel 231 miles using the faster mode of tranportation? Show your work or explain how you determined your answer

Answer 1

Faster mode: Car

Less time: 0.93 hour

Explanation:

Given

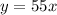`y = 55x` --- The equation of travelling by car

See attachment for missing details

Required

Determine by how much less time Lisa will travel 231 miles using the faster mode

First, we calculate the equation of travelling by train.

Start by calculating the slope (m)

`m=(y_2 - y_1)/(x_2 - x_1)`

Where

`(x_1,y_1) = (2,90)`

`(x_2,y_2) = (4,180)`

`m = (180 - 90)/(4-2)`

`m = (90)/(2)`

`m = 45`

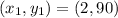
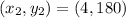
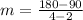
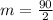
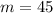
The equation is then calculated using:

`y = m(x - x_3) + y_3`

Where

`(x_3,y_3) = (6,270)`

`y = 45(x - 6) + 270`

`y = 45x - 270 + 270`

`y = 45x`

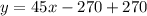
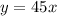
So, we have:

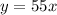`y = 55x` --- The equation of travelling by car

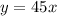`y = 45x` --- The equation of travelling by train

Next, we calculate the speed travelled using both means for 231 miles.

For travelling by car: Substitute 231 for y in
`y = 55x`

`231 = 55 * x`

`x = (231)/(55)`

`x = 4.20`

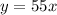
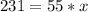
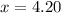
By car, Lisa travels for 4.20 hours

For travelling by train: Substitute 231 for y in
`y = 45x`

`231 = 45 * x`

`x = (231)/(45)`

`x = 5.13`

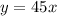
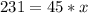
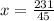
By train, Lisa travels for 5.13 hours

So, the faster mode of transportation is the car:

The less time is:

`5.13 - 4.20 =0.93\ hour`

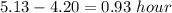
The less time spent is 0.93 hour