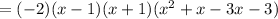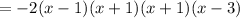Question

Factor the following equation -2x^4+4x^3+8x^2-4x-6

Answer 1

The factor of the quartic equation is:
`= -2(x-1)(x+1)^2(x-3)`

What is factorization of quartic equation?

Factorization is the simplification of a an equation into groups of similar factors within each groups. The equation can be a quadratic equation or a polynomial equation and there are several approach to solve them such as using:

• Factoring by grouping
• Rational Root Theorem
• Substitution method etc.

From the question given, we are to factor the quartic equation:

`= -2x^4+4x^3+8x^2-4x-6`

`= (-2)(x^4+4x^3+8x^2-4x-6)`

`= (-2)(x^4-x^3-x^3+x^2-5x^2+5x-3x+3)`

`= (-2)(x^3(x-1)-x^2(x-1)-5x(x-1)-3(x-1))`

`=-2(x-1)(x^3-x^2-5x-3)`

`(-2)(x-1)(x^3+x^2-2x^2-2x-3x-3)`

`=-2(x-1)(x+1)(x^2-2x-3)`

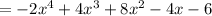
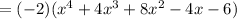
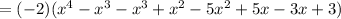
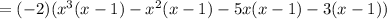
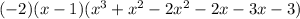
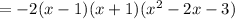
Factors are 1 and -3. The product is the factors are 1×(-3) = -3 and sum is 1 + (-3)= -2. So using 1 and -3 to split the -2 coefficient on the middle term, we have:

`=(-2)(x-1)(x+1)(x^2+x-3x-3)`

`= (-2)(x-1)(x+1)(x(x+1)-3(x+1))`

`=-2(x-1)(x+1)(x+1)(x-3)`

`= -2(x-1)(x+1)^2(x-3)`