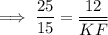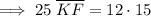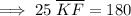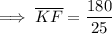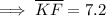Question

In the diagram DE || KL

Determine the length of DF and KF
show all work and round to nearest tenth

Answer 1

`\overline{DF}=13.3`

`\overline{KF} =7.2`

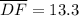
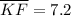
Explanation:

Vertical Angles Theorem

When two straight lines intersect, the opposite vertical angles are congruent.

Alternate Interior Angles Theorem

If a line intersects a set of parallel lines in the same plane at two distinct points, the alternate interior angles that are formed are congruent.

Given DE is parallel to KL.

According to the vertical angles theorem:

`\implies \angle\:\! D\:\!F\:\!E\:\! \cong\:\! \angle\:\! L\:\!F\:\!K`

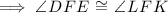
Therefore, according to the alternate interior angles theorem:

`\implies \angle\;\! D \;\!\cong\;\! \angle \;\!L`

`\implies \angle\;\! E\;\! \cong\;\! \angle\;\! K`

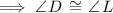
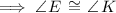
As all three angles of triangle DEF are congruent to the corresponding angles in triangle LKF, the triangles are similar.

In similar triangles, corresponding sides are always in the same ratio.

`\implies \overline{DE} : \overline{LK} = \overline{DF} : \overline{LF} = \overline{EF} : \overline{KF}`

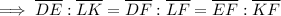
Given:

• DE = 25
• LK = 15
• LF = 8
• EF = 12

Therefore:

`\implies 25 : 15 = \overline{DF} : 8= 12 : \overline{KF}`

`\implies (25)/(15) = \frac{\overline{DF}}{8}= \frac{12}{\overline{KF}}`

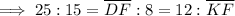
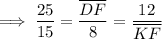
Solving for DF:

`\implies (25)/(15) = \frac{\overline{DF}}{8}`

`\implies \overline{DF}=(25 \cdot 8)/(15)`

`\implies \overline{DF}=(200)/(15)`

`\implies \overline{DF}=13.3\;\; \sf (1\;d.p.)`

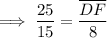
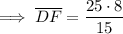
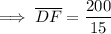
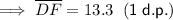
Solving for KF:

`\implies (25)/(15) = \frac{12}{\overline{KF}}`

`\implies 25\;\overline{KF} =12 \cdot 15`

`\implies 25\;\overline{KF} =180`

`\implies \overline{KF} =(180)/(25)`

`\implies \overline{KF} =7.2`

Answer 2

• DF = 13.3
• KF = 7.2

Explanation:

According to the diagram, triangles DEF and KLF are similar by AA postulate since two angles are congruent as alternate interior and one angle as vertical.

Corresponding sides of similar triangles are proportional.

It gives us ratios to solve for missing sides:

• DE/KL = DF/FL ⇒ 25/15 = DF/8 ⇒ DF = 8*25/15 ⇒ DF = 13.3
• DE/KL = EF/KF ⇒ 25/15 = 12/KF ⇒ KF = 12*15/25 ⇒ KF = 7.2