Answer:
4 small cars
7 large cars
Explanation:
To determine the number of small cars rented and the number of large cars rented by the group of college students, we can set up and solve a system of equations.
Let x be the number of small cars.
Let y be the number of large cars.
If the students rented 3 more large cars than small cars, then:
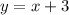
Given each small car can hold 4 people, each large car can hold 6 people, and the total number of people that the rented cars could hold is 58, then:
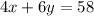
Therefore, the system of equations is:
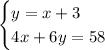
To solve the system of equations, substitute the first equation into the second equation and solve for x:
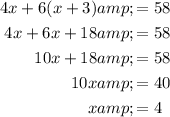
Substitute the found value of x into the first equation and solve for y:
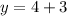
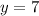
Therefore, the number of cars rented was: