Question

A group of college students are going to a lake house for the weekend and plan on renting small cars and large cars to make the trip. Each small car can hold 4 people and each large car can hold 6 people. The students rented 3 more large cars than small cars, which altogether can hold 58 people. Determine the number of small cars rented and the number of large cars rented.

Answer 1

4 small cars

7 large cars

Explanation:

To determine the number of small cars rented and the number of large cars rented by the group of college students, we can set up and solve a system of equations.

Let x be the number of small cars.

Let y be the number of large cars.

If the students rented 3 more large cars than small cars, then:

`y = x + 3`

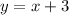
Given each small car can hold 4 people, each large car can hold 6 people, and the total number of people that the rented cars could hold is 58, then:

`4x + 6y = 58`

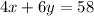
Therefore, the system of equations is:

`\begin{cases} y = x + 3\\4x + 6y = 58\end{cases}`

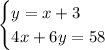
To solve the system of equations, substitute the first equation into the second equation and solve for x:

`\begin{aligned}4x+6(x+3)&=58\\4x+6x+18&=58\\10x+18&=58\\10x&=40\\x&=4\end{aligned}`

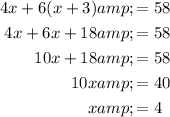
Substitute the found value of x into the first equation and solve for y:

`y=4+3`

`y=7`

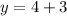
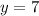
Therefore, the number of cars rented was:

• 4 small cars
• 7 large cars