Question

Find all solutions of cos x -sqrt = 0.

Answer 1

Option A

Explanation:

Good question!

We assume that x lies on the interval 0<=x<=360. We can therefore identify the solution in degrees:

`\cos \left(x\right)-√(1-3\cos ^2\left(x\right))=0,\:0\le \:x\le \:360^(\circ \:)`

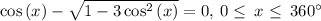
Now we can solve by substitution, and when simplified we get cos(x) = 1/2.

Take the inverse: x = cos^-1(1/2) = π/3 <--- angle in first quadrant

x = (2π-π/3) = 5π/3 <----- angle in fourth quadrant

As you know π/3 in degrees is 60, and 5π/3 = 360-60 = 300

Therefore your solution is the first option, x = 60+n360 and x = 300 + n360