Final Answer:
Substitution of a function under the root is:
![\[ (6x^2)/(√(3+2x^3)) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/b5b5bb6kj1zqo4h2hn87n0rjuldi9e46s3.png)
Step-by-step explanation:
In order to simplify the expression
 , we can employ the technique of substitution. Let
, we can employ the technique of substitution. Let
 , then the expression becomes
, then the expression becomes
 Now, to further simplify, we can rewrite the expression in terms of
Now, to further simplify, we can rewrite the expression in terms of
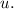
![\[ (6x^2)/(√(u)) = (6x^2)/(u^(1/2)) = 6x^2u^(-1/2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/3qyjuca05lvv0d9wr89zjpwt81tokg8z0t.png)
Next, differentiate
 . Now, substitute
. Now, substitute
 back into the expression:
back into the expression:
![\[ 6x^2u^(-1/2) = (du/dx)/(u^(1/2)) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/2fo89l2f4irtzxz0dvw3bjsj7zoalrg0ic.png)
Substitute
 to get the final expression:
to get the final expression:
![\[ (du/dx)/((3+2x^3)^(1/2)) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/n633l5fflyh9z1vi426pvvsp8pudgpfaqh.png)
Therefore, the simplified expression is
 . This substitution technique helps us express the given function in a more manageable form, making it easier to analyze and work with.
. This substitution technique helps us express the given function in a more manageable form, making it easier to analyze and work with.