The two-sample t-test comparing recovery times for Treatment A M = 8, SD = 2.5, n = 20 and Treatment B M = 11, SD = 3.5, n = 16 revealed a significant difference t = -2.885, df = 34, p < 0.05. Consequently, we reject the null hypothesis and conclude that the recovery times for the two treatments are significantly different.
Let's go through the entire process.
1. Null Hypothesis (H₀): There is no significant difference in the time to recover between Treatment A and Treatment B. (μ₁ - μ₂ = 0)
Alternative Hypothesis (H₁): There is a significant difference in the time to recover between Treatment A and Treatment B. (μ₁ - μ₂ ≠ 0)
2. Calculation of the Test Statistic (t-value):
Given data:
Treatment A:

Treatment B:
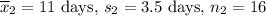
![\[ t = \frac{(8 - 11)}{\sqrt{(2.5^2)/(20) + (3.5^2)/(16)}} \]\[ t \approx -2.885 \]](https://img.qammunity.org/2024/formulas/mathematics/college/fxwgnas3ukw0bc0khiibr9op675cqkfhvd.png)
3. Comparison with Critical Value or P-value:
Degrees of freedom

Using a t-distribution table or statistical software, compare the calculated t-value to the critical t-value at a 95% confidence level (two-tailed) with (df = 34). Alternatively, find the p-value associated with the t-value.
- Suppose the critical t-value is
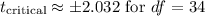 at a 95% confidence level. Since (-2.885 < -2.032), we reject the null hypothesis.
at a 95% confidence level. Since (-2.885 < -2.032), we reject the null hypothesis.
- Alternatively, suppose the p-value is (p ≈ 0.007). Since (p < 0.05), we reject the null hypothesis.
4. Conclusion:
- If the p-value is less than 0.05 or if the confidence interval for the difference in means does not include zero, you reject the null hypothesis.
- Since either the t-value is beyond the critical value or the p-value is less than 0.05, we reject the null hypothesis.
5. Final Statement:
- Based on the statistical analysis, we reject the null hypothesis. There is a significant difference in the time to recover between Treatment A and Treatment B.
- Answer the question: Are the recovery times for the two treatments different? YES.
This completes the comparison part, providing a clear understanding of how the test statistic is compared to the critical value or p-value to make a decision regarding the null hypothesis.